長岡 『東大の数学入試問題を楽しむ』を読んでみた
「読んでみた」シリーズについては以下の記事をご覧ください.
「読んでみた」シリーズ最初の記事です.
オリジナル版はこちら↓
出会いの経緯
私が現在通っている高校の図書委員会には,図書購入班というものがあります.
この班に入るとなんと!
自分の好きな本を書店で選び,学校図書館の蔵書に加えられるのです!!
もちろん本の購入にかかる代金は,学校の経費として落ちます.まさに一石二鳥.
この本とは,その図書購入班として,私が丸善を訪れたときに出会いました.
この本の著者である長岡亮介氏は,東進ハイスクールのカリスマ数学講師である長岡恭史の兄で,自身も駿台のカリスマ数学講師として活躍していました.
私は東京大学が第一志望ではありませんが,「本質的で興味深く面白い」問題を毎年入試問題として出題する,東京大学の「一種のひねくれ根性」を味わいたいと思い,この本を選びました.
この本について
基本情報

タイトル:東大の数学入試問題を楽しむ 数学のクラシック鑑賞
定価:2200円(税抜)
発行年月:2013年2月
判型:A5判
ページ数:304ページ
内容紹介
東大の入試問題は、数学的奥行き・広がりをもった良問が多い。すなわち“古典”である。単に解法を知るのでなく、入試の古典から「之を知る者は之を楽しむ者に如かず」の精神を学び、真の“数学力”を身につけよう。
著者
1947年 長野市生まれ
1977年 東京大学大学院理学研究科博士課程を満期退学,数理哲学,数学史を専攻.
その後,津田塾大学助教授,大東文化大学教授,放送大学教授を経て,明治大学理工学部数学科特任教授.2017年退職.
現在,若手数学教育者を支援する組織TECUMを主宰.(2020年4月現在)
こんな人にオススメ
本文中に登場する東京大学の数学入試問題は,あくまで「本文の補助」なので,数学が得意でない方や嫌いな方,内容を忘れてしまった方でも十二分に楽しめます.
もちろん,数学ⅠAⅡB履修済み(高校1~2年生程度)だとより楽しめます.
本書を読むうえ必要なものは,「自分で考え抜く力」ただ一つです.
よく学校の先生は
「10分考えてわからなかったらそれ以上考えても無駄だから答えを見よう」
と言いますが,私からしたら
それは全くの見当違い
です.
考える時間・考え続ける時間は,一分一秒あなた自身の宝になります.
もちろん入試などの時間制限がある場では,より柔軟に,問題を処理する能力が必要だとは思いますが.
感想
まず伝えたいのは,
参考書・数学書の垣根を越えて,すべての「教育をする者」「教育を受ける者」にこの本を読んでほしい
ということです.
「数学とは,どんな世界なのであろう?」「数学を学ぶことには,どんな意味があるのだろう?」「数学が好きになるために,何をしたらよいのだろう?」――本書は,筆者が,これまでに何度も訊ねられ,一度もうまく答えることができていない,このような,「ふつうの人」からの質問に答えるための試みである.
――― 長岡亮介著「東大の数学入試問題を楽しむ はじめに」より引用
これは,冒頭に書かれている筆者のねらいです.
本書は上記の問いかけに対して,明確に答えているわけではありません.
しかし一読したらわかるように,本書のあらゆるところで「筆者の考え方の一つ」や「筆者の回答の一つ」がちりばめられています.
ある種の「寓喩」です.
そのような問いに対する「実体の持たない,輪郭のつかめない」答えを,東大の数学入試問題を絡めた物語を通して伝えようという気概が,この本から感じ取れました.
「良い問題を1題作る」のは「良い曲を1曲作る」のと似ている
と,聖光学院時代の同級生である元オフコースの小田和正氏が本の帯に寄せています.
上記の内容紹介では,数学に焦点を当てていますが,個人的には,数学の本というより,哲学的・思想色が強めな本だと感じました.それ故「大学受験参考書」としては賛否あるものと思われます.
しかし,この本に書かれている「数学の考え方」は,職業数学に限らず,大学受験にも役立つことを私が保証いたします.読んで,考えて,"絶対に"損はしません.
私自身数学をやっているときに,
「なぜ私は数学をやっているのか?」
「私より才能に恵まれている人が限りなく多く存在するのに,私が数学をやる意味はあるのか?」
などと考えることが(現在も)あります.
そんな私に,少しの勇気と自信を与えてくれたのが,この本です.
ここで私も著者になったつもりで,上記の問題に対する回答を与えてみたいと思います.
数学は「自然科学と哲学の緩衝材」です.
緩衝材であるからこそ,科学者は数学を用いて現象の説明に勤しみ,哲学者はゲーデルの不完全性定理(自然数論の理論が不完全であること)に代表される数学の基礎に魅了されます.
This book is written in the mathematical language.
これは,ガリレオ・ガリレイが残したとされる格言です.
私は「あらゆるものが数学で出来ている」というような過激な主張はしませんが,
この世界を極度に抽象化した先に数学がある
と考えています.
数学は「芸術」でもあります.
世界を抽象化したものだから,人間は数学に対して何らかの魅力を感じますし,数学はある種の芸術として成立するのです.
これが,私の考える「数学」です.
--閑話休題--
これからは本文中で印象に残った話を,全41話の中から3話(digest版では1話)pick upしてご紹介します.
第9話 理系 vs. 文系?!
高校生にとって「理系か文系か?」という問いは,様々な場面で登場する,とてもセンセーショナルな議題ですね.
どちらが「優れているか(頭が良い,能力が高いetc.)?」などを,理系文系で区別して考えている人も一定数います.
また「理学部は就職無理学部」「数学が苦手だから文系」などのステレオタイプ思考が,日本では至る所に見られます.
(現在私が通っている学校でも,「理系・文系の"見えない壁"」が絶賛建設中.)
実際にそうでしょうか?
筆者はスノー著「2つの文化と社会革命」の有名な箇所を原文で引用して,このように述べました.
A good many times I have been present at gatherings of people who, by the standards of the traditional culture, are thought highly educated and who have with considerable gusto been expressing their incredulity at the illiteracy of scientists. Once or twice I have been provoked and have asked the company how many of them could describe the Second Law of Thermodynamics. The response was cold: it was also negative. Yet I was asking something which is about the scientific equivalent of : Have you read a work of Shakespeare's ?
I now believe that if I had asked an even simpler question ー such as, What do you mean by mass, or acceleration, which is the scientific equivalent of saying, Can you read ? ― not more than one in ten of the highly educated would have felt that I was speaking the same language. So the great edifice of modern physics goes up, and the majority of the cleverest people in the western world have about as much insight into it as their neolithic ancestors would have had.
「数学が苦手だから文系」「英語が嫌いだから理系」といった進路選択が一部にあると聞くが,そのような主張が馬鹿げていることを知ってもらうためには,こういう「英語」で「理解」するとはどういうことなのか考えていただけば十分であろう.実際,単なる英語好きの「文系」ではスノーの嘲笑の的になるのが関の山,単なる「理系」では,この程度の短文ですら手も足も出ないであろうからだ.
(中略)
実は,今日,「理系 vs. 文系」という分類自体が,すでに古くさい.
――― 長岡亮介著「東大の数学入試問題を楽しむ 第9話」より引用
文章の通り,単なる数学好きの「理系」である私は,この英文に手も足も出ませんでした.反省
知識の細分化が進んだ現在,スペシャリストは地球上に数えきれないほど多く存在します.
生物学も「細胞生物学,分子遺伝学,分子生物学,進化生物学,生態学」などの分野に細分化されていますね.
このように,現在の学問は縦方向に深くなっていますが,横方向のつながりが失われてしまう可能性を常に孕んでいます.
昔の偉人たちは,いろいろな学問を兼任していました.
アルキメデスは,数学者,物理学者,技術者,発明家,天文学者であり,
レオナルド・ダ・ヴィンチは,音楽,建築,絵画,数学,解剖など,様々な分野で顕著な成果を残しています.
昔は現在ほど学問が専門性を帯びていませんでしたが,それでもなお,幅広い教養の大切さは今も訴えられ続けています.
大学1年次などの教養科目の必要性はここにあるのでしょう.
グローバル化,機械化,AIの進化が進む中で,人間として本当に必要な能力とは何なのか?
是非皆さんも,この本を手に取って一緒に考えてみませんか?
手引き
この章では,本書に載っている問題の解答とは違う「オリジナルの別解」について紹介・解説していきます.(digest版では,問題を解く際のキーポイントのみ紹介します)
第41話 小さなムラを出て《大きな世界》へ
1996年度理科第3問
問題は著作権の都合上,下記のリンク先でご覧ください.
(1)は,球面上の接平面より上側が,その点から見える空間です.(問題の文末にもきちんと数学的に定式化されています)
私たちの感覚と経験からも,これは正しい定式化ですね.
問題は(2)です.
リンク先の解答例では,適切な式変形をある意味愚直に施していき,答えを求めています.
しかしこの解答だけで終わるのはつまらないので,もう一つ「直感的で面白い」別解を与えようと思います.
キーポイントは
「S上の点Pから立方体の頂点を見るのではなく,立方体の頂点から見える範囲を球面S上で描写する」
です.
気になる方は,ぜひオリジナル版へ遊びに来てください!
まとめ
最後までご覧いただきありがとうございました.
次回の記事もお楽しみに!
参考文献
東大の数学入試問題を楽しむ(本) - 日本評論社
東大の数学入試問題を楽しむ|日本評論社
https://www.nippyo.co.jp/shop/book/6116.html
https://pchira.wicurio.com/index.php?%E9%95%B7%E5%B2%A1%E4%BA%AE%E4%BB%8B
【数学の考え方(全六回)】第二回 ≦ と < の小さな違い・大きな違い ~数学の厳密さ~
数学の考え方とは?
「数学の考え方」では,全六回に及び
を丁寧に解説していきます.
数学の「基礎中の基礎」から取り扱い,少しずつステップアップしていくので,
などなど,皆さん大歓迎です!
ぜひ,私と一緒に楽しみながら数学していきましょう!
全六回の記事一覧です.
- 第一回 たし算・かけ算から学ぶ計算のしくみ
- 第二回 ≦ と < の小さな違い・大きな違い(←now!!)
- 第三回 小中高の算数・数学からわかる!一般化のはなし
- 第四回 幾何学はたった「5つの約束」でできている!?
- 第五回 もう忘れない!必要条件・十分条件の見分け方
- 第六回 必見!!こんなに面白い数学史
それでは,Let's math!
不等号のはなし
皆さんは「不等号」と聞いたら,何を思い浮かべますか?
きっと多くの方は,ひらがなの「く」のような記号を思い浮かべるでしょう.
(ex)
a < b:aはbより小さい(bはaより大きい)
a > b:aはbより大きい(bはaより小さい)
a ≦ b:aはb以下(bはa以上)
a ≧ b:aはb以上(bはa以下)
etc.
「等号」という単語の頭に打消しの「不」がついているので,不等号は「等しくないこと」を表す記号だと考えている人が多いと思います.
しかし,その解釈は少しだけ不正確です.
(ex)
1は2より小さい(2は1より大きい) → 1 < 2
1は3以下(3は1以上) → 1 ≦ 3
4は4以下(4は4以上) → 4 ≦ 4
三つ目の例は,等しい数字が不等号で結ばれていて少し違和感を覚えるかもしれません.
しかし,実はこの表記も数学的に正しい!
不等号の本質は「大小関係を表すこと」なのです.

このように,言葉で説明する代わりに不等号を用いると,主張する内容をとても簡潔な形で述べることができますね.
体験談
ここで一つ,第二回の導入ついでに,個人的な体験談を紹介します.
これは,私が中学1年生の頃の出来事です.
授業の合間の休み時間,私は数学の先生に次のような質問をしました.
「x < 100 と x ≦ 99 って同じじゃないんですか?」
Q.
「x < 100」と「x ≦ 99」
2つの式の違いは何でしょうか?
振り返ってみると,これほど「アタリマエ」な質問はないでしょう.
しかし当時の私は,この2式の違いが何か,純粋に気になっていました.
先生は,こんな「アタリマエ」な質問に対しても
「99.5はどうかな?」
と,優しく答えてくれました.
A.
99 ≦ x <100 の範囲が含まれているかどうかの違い
その返答を聞くや否や,私は誤りを自覚し,お礼を言い,恥ずかしがりながら先生の元を去るのでした...
この「一見アタリマエに思える質問」も,実はきちんとした意図がありました.
私は当時,二つの不等式を「整数の世界」で考えていたのです.
実際に,整数の世界で二つの不等式を比べてみましょう.
x < 100 は「100より小さい整数」つまり,99,98,97,...
x ≦ 99 は「99以下の整数」つまり,99,98,97,...
どちらも同じく,99以下の整数を表しています.
つまり,
実数の範囲では意味の異なる不等式が,整数の範囲では同じ意味になる
ということです.
先生の返答を聞いたとき,私は初めて「数学」というものを肌で感じました.
この経験を通して,私は「整数の世界」の住人から「実数の世界」の住人になり,
とびとび(離散的)な心が,なめらか(連続的)な心に成長したのです.
以上が私の体験談でした.
思えばこの質問が,数学の道を志すことになったターニングポイントだったのかもしれません.
第一回の記事で述べた「アタリマエを疑う」姿勢は,この体験をもとに書かれています.
話は変わりますが,先ほどの質問を少し変え
Q.
「x < 100」と「x ≦ 100」
2つの式の違いは何でしょうか?
としたらどうでしょうか.
こちらの違いは「100が含まれているかどうか」だけですね.
しかし,本当にそれだけの違いなのでしょうか?
もちろんここで思考を中断してもいいですが,それではやはり味気ないので,この「アタリマエに見える単純な疑問」を一緒に深掘りしていきましょう.
不等号の境界を探検
不等号に関する式 x < (ある数字)は,x の集合を表しています.
(ここで言う集合は,数の集まりのことを指します.)
(ある数字)を境目に,集合に含まれているか否かが定まる訳です.
この節では,不等式で定められる集合の境目(境界)を一緒に冒険していきましょう!

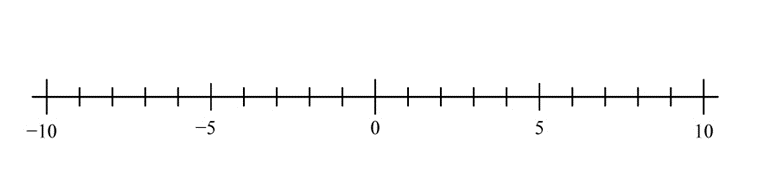
上の図は,x < 100 を数直線上に表し,視野を拡大していったものです.
この図から分かることは何でしょうか?
それは,「いくら進んでもゴールが存在しない」ということです.
ゴールが存在しないというのは,境界となる数字が不等式で定められている集合内に含まれていないという意味です.
(ex) x < 100 の場合
境界となる数字100は,x < 100 の集合に含まれていない.
集合内から100というゴールに向かう場合,
99 → 99.9 → 99.99 → ... と,100に限りなく近づくことはできる.
しかし,100自身にはなれない.
つまりこの場合,集合内から100というゴールには永遠にたどり着けない.
つまり,x < 100 の場合は「集合に最大値が存在しない」と言い換えられます.
以上のことから,
等号がついていれば,集合は最大(最小)値が定まる「カッチリと・正確な」ものであり,
等号がついていなければ,集合は最大(最小)値が定まらない「ふわっと・曖昧な」ものである
ことがわかりました.
等号の「アリ・ナシ」という形式の差異が,「カッチリ・ふわっと」という概念の差異を生み出すのは,非常に興味深いことだと個人的には思います.
小さな違い・大きな違い2選
先ほどの例では,不等号の「く」の字の下に等号(=)があるかないかの些細な違いが,決定的な変化を引き起こしていました.
このような,
「一見似ていて,実はまったく違う概念」
は,先ほどの例以外にも数多く存在します.
今回はそのような概念の中から2つピックアップし,
「どのような些細な違いが,どのような決定的な変化をもたらすか」
についてわかりやすく解説していきます.
等号(=)と不等号(<)
一番最初の例では < と ≦ の違いに着目しましたが,今回の例では等号と不等号の違いに注目します.
等号と不等号に関しては,以下ような基本性質が知られています.
等号
不等号
これら二つの性質は一見,非常に似ています.
等号を不等号に置き換えただけのようにも見えますね.
しかし,これらをそう簡単に同一視してしまうと,そこで数学の世界は終わってしまいます.
ここは,第一回の記事通りに「アタリマエ」を疑っていきましょう.
Q.
等号と不等号の決定的な違いは何でしょうか?
A.
扱える情報量の違い / 対称律が成り立たない
名前が似ている等号と不等号ですが,
実は,等号と不等号では扱える情報量が天と地の差なのです.
等号は「〇と△はピッタリ等しい」という,正確さを表すのに対し,
不等号は「〇より△の方がだいたい大きい(小さい)」という,曖昧さを表します.
また,等号で成立する
という法則が,不等号では
となり,成立しません.
この法則のことを,数学用語で「対称律」と呼びます.
要するに「両辺を入れ替えても関係は保たれるか」ということです.
「右辺と左辺を入れ替えられるかどうか」が,とても重要という訳ですね.
その分不等号は,等号よりも両辺を結ぶ関係が弱いといえます.
しかし,等号に比べて「関係が弱く,曖昧である」という特徴は,不等号の強みでもあります.
Q.
198(円/個)のリンゴ3個と,1470(円/房)のブドウ2房を買うには,何円所持していればよいか?
A.
198 < 200,1470 < 1500 と見積もると,
(198 × 3) + (1470 × 2) < (200 × 3) + (1500 × 2) = 3600
つまり,3600円所持していれば大丈夫
四捨五入や上記のようなお会計の概算などの近似計算は,不等号の強みが生かされる最たる例です.
(近似計算とは,切り上げ・切り捨て・四捨五入などを駆使して,真の値に近い値を求める計算のこと)
その点不等式は,より日常生活に寄り添った数学と言えるでしょう.

有理数と実数
有理数と実数は,どちらも第一回の記事で四則演算が定義できる数の集合として紹介しました.
たし算・かけ算しかできなかった自然数が,ひき算もできる整数の集合に広がり,さらに,わり算もできる有理数へと進化する.
この「様々な計算ができる便利さ」を求めて数の世界が広がる過程は,とても理解しやすいですね.
しかし,実数はどうでしょう.
実数は有理数と同様に四則演算ができる数の集合です.
そして「無理数」という,有理数には含まれず実数には含まれる数が存在します.
しかし,無理数であるルート2やπなどは,日常生活ではめったに使いません.
ではなぜ,実用性のない実数の世界ができたのでしょうか?
有理数と実数の明確な違いは何なのでしょうか?
Q.
有理数の集合と実数の集合は,どのような点で決定的に違うのでしょうか?
A.
有理数よりも実数の方がなめらか
第一回では問題のみを提示して,答え合わせをしていませんでしたね.
(なめらかとは,連続であるということ)
(ex)
→ 1/2 と 1/3 の真ん中は,(1 / 2 + 1 / 3) / 2 = 5 / 12 で有理数となる)
しかし,第一回の記事でも述べた通り,数直線上の数は有理数だけでは取りつくすことができません.
しかも無理数は,有理数と同様に有限の区間にも無限個存在することが知られています.
つまり,有理数は無限個存在していて,数直線上では有理数の集合だけで直線をなすように見えますが,実際は
無理数という隙間が無限個存在しているとぎれとぎれの集合
なのです.
その点実数は,有理数と無理数の集合が合わさった,とても滑らかな集合のように感じませんか?
「隙間だらけの有理数は,隙間を埋めたいという気持ちで実数を構成した」
この「隙間を埋めたい」気持ちは,人間の「心の隙間を埋めたい」気持ちとよく似ていて面白いですよね.
数学の厳密さ
些細な違いが決定的な変化をもたらす例として,
「 ≦ と < 」「等号と不等号」「有理数と実数」
の計3種類を取り上げました.
これら3つの組はそれぞれ,
「不等号の「く」の字の下に等号がついているか,ついていないか」
「等号という熟語の前に「不」という漢字がついているか,ついていないか」
「無理数が集合に含まれているか,含まれていないか」
という,形式のわずかな差異から生まれる
「集合の境界がカッチリ・正確か,ふわっと・曖昧か」
「両辺の関係が強く・正確か,弱く・曖昧か」
「数の集合として滑らかか,隙間だらけか」
という,概念の大きな変化がありました.
これらの例を通して伝えたかったことは,
についてです.
少しの違いが大きな変化をもたらすことは,(数学だけに限らず)あらゆる物事で往々にしてあります.
些細な部分を気にしないというおおらかさも時には必要ですが,それ以上に学問の発展には,多くの人達による「徹底的な不寛容の努力」が欠かせませんでした.
似ている概念を同一視することは,もちろん大事です.
ですが,似ている概念の異なる点をきちんと意識して,その差異を数式や言葉で表現することも,数学において非常に重要なプロセスといえます.
「少しの違いも見逃さないこと」が数学の厳密な点であり,他の学問にはあまり見られない特色です.
もちろん「数学は厳密さがすべてだ」と主張している訳ではありません.
なんでも最初から「厳密厳密」と,細部ばかりにこだわってしまうと,想像力の存在しない,退屈な「勉めて強いられる」勉強になってしまいます.
なので学校では,児童・生徒の健全な成長のために,定義や概念の正確さを多少犠牲にしてでも教えていますよね.
最後に二つの言葉を残して,今回の記事を締めくくろうと思います.
広大な世界へ...
極限と ε-δ 論法
人類は長い歴史の中で,厳密な数学を獲得してきました.
その中で最も基礎的で重要なものが,節の見出しにもなっている
ε-δ(イプシロン - デルタ)論法 です.
ε‐δ 論法のステートメントは少しゴツいので,今回は ε‐δ 論法の「気持ち」だけでも紹介したいと思います.
ずばり,ε‐δ 論法とは「極限を厳密に定式化したもの」です.
極限 を,高校数学では
「x が a に限りなく近づくとき,f(x) は A に限りなく近づく」
のような,直感的な説明だけで済ませています.
しかし「限りなく近づく」という言葉が数式で定義されていない以上,この説明は厳密さに欠けています.
そのギャップを埋めるために存在するのが,他ならぬ ε‐δ 論法なのです.
この論法は自然の直観を正確に定式化したものなので,気になる方は実際のステートメントを見て,意味をよく考えてみてください.
自力で理解しようとする不断の努力は,必ずあなた自身の宝物になりますよ!

まとめ
今回のキーポイント
- 形式の細かい違いが,概念の大きな変化につながることもある
- 数学らしさは,その厳密さに起因している
- ε-δ 論法は,自然な考えを定式化したもの
最後までご覧いただきありがとうございました.
次回の記事もお楽しみに!
参考文献
かわいいフリー素材集 いらすとや
Wikipedia いろいろ
初心者から始める!競技プログラミング
オリジナル版はこちら↓

この記事では,プログラミング・パソコン初心者の私が,事前に知っておいて良かった情報や実際につまづいたポイントを,初心者にもわかりやすく「等身大」で説明いたします.
競技プログラミングについて
競技プログラミングとは?
競技プログラミング(以下競プロ)とは,コンピュータプログラミングの能力や技術を競い合う「プログラミングコンテスト」の一種です.
参加者全員に同一の課題が出題され,より早く与えられた要求を満足するプログラムを正確に記述することを競います.
コンテストはインターネット上の各種ウェブサイトで,週一回ほどの周期で定期的に開催されています.
有名な競プロサイト
この節では,主要・有名な競技プログラミングコンテストのサイトを紹介します.
今回は,
- AtCoder(アットコーダー)
- Topcoder(トップコーダー)
- Codeforces(コードフォースィズ)
の,以上三種類のサイトについて簡単に説明します.
1. AtCoder
AtCoderはAtCoder株式会社が提供している,日本発のプログラミングコンテストサイトです.
週一回のペースで何かしらのコンテストが開催されています.
また「AtCoder Problems」や「AtCoder Scores」といった,とても便利な外部ウェブサイトが充実しています.
加えて,C++プログラミング初心者のためのオンライン入門教材(APG4b)も存在していて,初心者でも始めやすい環境が整えられています.
外国のサイトと違い,質の高い問題が日本語で提供されるので,日本人には嬉しいですよね.
2. Topcoder
TopcoderはAppirio社が提供している,アメリカ発のプログラミングコンテストサイトです.
今回紹介している3つのサイトの中では最も長い歴史を誇ります(2001年~).
登録するまでは簡単ですが,参加までの手順が他の大会と比べて少し面倒くさい(らしい?)です.
3. Codeforces
CodeforcesはITMO Universityに所属するMike Mirzayanovさん達が実施している,ロシア発のプログラミングコンテストサイトです.
およそ85000人ものユーザー数(2020年5月現在)を誇る,世界で最も規模の大きいコンテストサイトです.
コンテストの開催頻度が非常に高いのが一番の魅力ですね.
競プロのはじめ方
今回の記事では,競プロの「初心者にはオススメしない」はじめ方を説明します.
初心者にオススメしないはじめ方
これから紹介するポイントを押さえておけば,競技プログラミングを楽に・簡単に始めることができます.
以下の二つが,今回説明する「初心者に注意してほしいポイント」です.
1. PC上でプログラミング言語(特にC/C++)の環境構築をする
競プロを紹介しているサイトでは,まず初めにLinuxなどを用いたプログラミング言語の環境構築を勧めています.
自分の書いたプログラミングコードを手元でテストできると便利ですからね.
私は,初心者にこの方法は全くお勧めしません.
私自身,UbuntuやVScodeなどのアプリケーションを自分のパソコンにダウンロードし,必死に環境構築を頑張ってみました.
しかし,C言語の環境構築はできても,C++の環境構築はまったく上手くできませんでした...
このような,競プロではない「非本質的で煩雑な作業」を,パソコンの扱いに不慣れな人がやろうとすると,とても大きな負担になり,モチベーションも下がってしまいます.
幸運なことに,現在は自分のPC上で環境構築をしなくとも,AtCoderのコードテストやWandboxなどの,ブラウザ上で稼働する「オンラインコンパイラ」があります.

これを使えば,競プロは(少なくとも初級者のレベルでは)問題なく始められるでしょう.
実際に私も,現在はオンラインコンパイラで競プロを楽しんでいます.
2. はじめから高すぎる目標を持つ
競プロをはじめる理由は人それぞれ,多種多様です.
「プログラミング言語を学び,使いこなせるようになりたい」人や「オンライン上で世界中の人たちと対戦してみたい」人,はたまた「ただの暇つぶし」という人もいるでしょう.
しかし,ほとんどの人は「より高いレベル」,AtCoder の用語でいうとより高いレーティング・色を目指していると思います.
競プロ界隈では,レッドコーダーと呼ばれる,プログラミング界の「神」のような存在がいます.
最初から「レッドコーダーを目指す!」という壮大な目標を立てても,そのモチベーションは永遠には続きません.
できるだけ短期的な,長くとも1年以内の目標を持つとよいでしょう.
私は1年以内に,水色コーダー(レート1200以上)到達を目指して,現在頑張っております.
(応援してくれたら嬉しいです...)
まとめ
とても気軽に始められて,どっぷりとのめり込むことができるのが競プロの良さです.
年齢や理系文系関係なしに,遊び感覚で論理的思考力を鍛えることができます.
また,最近は競プロを通した転職・就職活動も盛んで,やって損をすることはないと断言できます.
この記事を読んで,少しでも競技プログラミングが気になった方は早速登録してみてくださいね!
↓下のリンクから,AtCoderの新規登録ができます.(もちろん無料です!!)
最後までご覧いただきありがとうございました.
次回の記事もお楽しみに!
オリジナル版はこちら↓
参考文献
Wikipediaいろいろ (競技プログラミング,プログラミングコンテストetc.)
Topcoder - https://www.topcoder.com
Codeforces - https://codeforces.com
AtCoder コンテストについての tips - https://qiita.com/drken/items/8a6f139158cde8a61dce
C++入門 AtCoder Programming Guide for beginners (APG4b) - https://atcoder.jp/contests/apg4b
【数学の考え方(全六回)】第一回 たし算・かけ算から学ぶ計算のしくみ ~アタリマエを疑う~
ブログを始めてから初めて,私のブログが対象としている「読者の基準」が明確でないことに気づかされました.
その問題を解決するための新シリーズです.
オリジナル版はこちら↓
数学の考え方とは?
「数学の考え方」では,全六回に及び
を丁寧に解説していきます.
数学の「基礎中の基礎」から取り扱い,少しずつステップアップしていくので,
などなど,皆さん大歓迎です!
ぜひ,私と一緒に楽しみながら数学しましょう!
全六回の記事一覧です.
- 第一回 たし算・かけ算から学ぶ計算のしくみ(←now!!)
- 第二回 ≦ と < の小さな違い・大きな違い
- 第三回 小中高の算数・数学からわかる!一般化のはなし
- 第四回 幾何学はたった「5つの約束」でできている!?
- 第五回 もう忘れない!必要条件・十分条件の見分け方
- 第六回 必見!!こんなに面白い数学史
それでは,Let's math!
四則演算(+,-,×,÷)の復習
皆さんは「四則演算」をご存じでしょうか?
四則演算とは
- たし算(加算,+,addition)
- ひき算(減算,-,subtraction)
- かけ算(乗算,×,multiplication)
- わり算(除算,÷,division)
計4つの演算のことをいいます.
(かけ算の記号は「・」と表記されたり,省略されたりします.)
(この記事では,演算=計算と解釈しても大丈夫です.)
皆さんも日常生活で,買い物や割り勘などをするときによく計算しますよね.
Q.
一部屋1000円のカラオケボックスを4人で借りるとき,
一人何円ずつお金を払えばよいか?
A.
1000(円)÷4(人)=250(円/1人)
しかし,異なる演算子(+,-などの記号)が1つの式に含まれている場合では,計算する順序によって答えが変わることがあります.
Q.
12÷3-2
A1. (12÷3)-2=4-2=2
A2. 12÷(3-2)=12÷1=12
このような問題を解決する,つまり
ために生まれたのが,小学校で習う「計算のルール」です.
計算のルール
- かっこの中から計算する
- かけ算・わり算はたし算・ひき算より先に計算する
- かけ算・わり算のみの式は前から計算する
- たし算・ひき算のみの式も前から計算する
計算のルールを一通り確認し終えたところで,練習問題に挑戦しましょう.
Q.
12÷4+(3×2-4)×5=?
A.
12÷4+(3×2-4)×5
=3+(6-4)×5
=3+2×5
=13
次の問題はどうでしょうか.
Q.
6÷2(1+2)=?
A.
考え方による
→ 1 or 9
実はこの問題,ネット上で議論を巻き起こした問題なんです.
この問題を引き起こしている原因は,簡単に言うと「解釈の違い」です.
詳細はリンク先のサイトを参照してください.
私は,後者のような「個人の解釈」によって答えが一意に定まらないものについて,「数学的に考える必要がない」と思っています.
四則演算の世界
私と一緒に自然数から始まる数の世界を冒険していきましょう!
数の世界の始まりと自然数
数の起源は自然数で「ものを数えるために生まれた」と考えられています.
人間が自然に考えついた数なので「自然数」と呼ばれているらしいです.
日本では正の整数(1,2,3,4,etc.)を自然数と定義していますが,
フランスなどでは非負整数(0,1,2,3,etc.)を自然数と定義しています.
位取り記数法について
位取り記数法とは,数の表現方法の一種で,あらかじめ定められた何種類かの記号や数字を並べることによって数を表す方法です.
例えば,日本人を含む多くの人類が現在使用している10進法では,10種類のアラビア数字(0,1,2,3,4,5,6,7,8,9)を横に並べることによって,数を表しています.
(数字の代わりに数種類のローマ字(a,b,c,d,etc.)を利用する場合もあります.)
「10進法なんて当たり前」と思う人もいるかもしれませんが,実はそれほど当たり前ではありません.
たまたま人間の指の本数が合計10本だったので,10進法を利用しているだけなのです.
実際に,メソポタミア文明では60進法,マヤ文明では20進法が利用されていました.
60や20の由来が気になる方はぜひご自身で調べてみてください.
特に,60進法は現在でも時間(時・分・秒)をあらわすときに使われていますよね.
Q.
2本指の宇宙人は何進法を使っているでしょうか?
自然数とたし算・かけ算の世界
私たちの知っている数は自然数のみとします.
自然数の世界のみで出来る計算はあるでしょうか?
試しに,自然数の世界でたし算をしてみましょう.
(ex)
1+1=2
3+4=7 etc.
Q.
A.
常に自然数
このように,たし算は自然数の世界のみで計算が成り立ちます.
かけ算でも試してみましょう.
(ex)
2×3=6
3×5=15 etc.
Q.
A.
常に自然数
こちらもたし算と同様に,自然数の世界のみで計算が成り立っています.
このような場合,自然数の集合はたし算とかけ算について閉じていると言います.
閉じているとき,自然数の集合上でたし算とかけ算は定義できるのです.
「その世界だけで完結している(成り立っている)」というイメージが,閉じているという言葉に現れていますね.
Q.
なぜ自然数の定義に0を含めても含めなくてもよいのでしょうか?
キーワード:閉じている
Q.
「自然数は-1以上の整数」という人がいないのはなぜかを自由に論じなさい。(自明大学2019入試より抜粋)
— 結城浩 (@hyuki) 2019年2月19日

整数とひき算の世界
私たちは現在,自然数の世界までを知っています.
試しに,自然数の世界でひき算をしてみましょう.
(ex)
3-2=1
5-9=? etc.
Q.
A.
自然数とは限らない
自然数の世界のみで計算しているので,1(または0)より小さい数は存在しません.
このように,ひき算は自然数の世界だけでは成り立ちません.
この場合,自然数の集合はひき算について閉じていないといいます.
閉じていないとき,自然数の集合上でひき算は定義できないのです.
これは不便です.家計のやりくりもできません.
現代人は負の数の概念に対して抵抗を感じないかもしれませんが,「人間は考える葦である」で有名な大天才パスカルでさえ,負の数の概念は理解できませんでした.

そこで私たちは,自然数の集合をより使いやすい(ひき算ができる)数の集合に進化させようと考えます.
この「便利になりたいよう」という感覚が,数学の情緒というものです.
そして私たちは試行錯誤して整数の世界を発見します.
整数とは「0 とそれに 1 ずつ加えていって得られる自然数 (1, 2, 3, 4, …) および 1 ずつ引いていって得られる数 (−1, −2, −3, −4, …) の総称」のことです.
なので,整数の世界は自然数の世界を含んでいます.(自然数の集合 整数の集合)
整数の世界で,ひき算はできるのでしょうか?
Q.
(整数)-(整数)は整数でしょうか?
A.
常に整数
新しい数の世界である整数の世界では,ひき算ができるようになりました.
整数の集合はひき算について閉じている,つまり,整数の集合上でひき算は定義できるというわけです.
同様に整数の集合はたし算・かけ算についても閉じています.
つまり,整数の集合上でたし算・かけ算・ひき算は定義できます.
こうして私たちは,自然数よりも使い勝手の良い整数を手に入れることができました.
有理数とわり算の世界
私たちは,自然数の世界を含む,より大きな整数の世界を手に入れました.
今度はわり算です.
果たして,整数の世界でわり算はできる(整数の集合について閉じている)でしょうか
(ex)
6÷3=2
5÷3=? etc.
Q.
(整数)÷(整数)は整数でしょうか?
A.
整数とは限らない
整数の世界で計算しているので,分数は存在しません.
このように,わり算は整数の世界だけでは成り立ちません.
わり算は自然数の世界でも同様の理由で成り立ちません.
ここで再び登場するのが「もっと便利になりたいよう」という数学の情緒です.
そして試行錯誤して,私たちは有理数の世界を発見するわけです.
有理数とは,整数の比で表される数,つまり分数のことです.
なので,有理数の世界は整数の世界を含んでいます.(整数の集合 有理数の集合)
有理数の世界で,わり算はできるのでしょうか?
Q.
A.
常に有理数
より新しい数の世界である有理数の世界では,わり算ができるようになりました.
有理数の集合はわり算について閉じているというわけです.
同様に,有理数の集合はたし算・かけ算・ひき算についても閉じています.
つまり,有理数の集合上で四則演算は定義できるのです.
こうして私たちは,整数よりも使い勝手の良い有理数を手に入れることができました.
無理数,そして実数へ...
数の世界の冒険も,もうそろそろ終盤です.
学校では数の大小関係などについて学ぶとき,よく数直線が用いられます.
私たちは現在,有理数の世界までを知っています.
Q.
有理数のみで数直線上の数を取りつくすことができるか?
A.
できない
なんと,数直線上には無理数という,整数の比で表すことのできない数が存在します!
(ex)
ルート2=1.41421...
円周率π=3.14159...
自然対数の底e=2.71828...
etc.
学校では,背理法を使う練習として「ルート2が無理数であることの証明」がよく取り扱われていますね.
この無理数の集合と有理数の集合を合わせると,実数の集合になります.
有理数の集合を「完備化」して実数の集合にすると考えると現代的.)
有理数の集合が進化した実数の集合は,数直線上の数を取りつくすことができます.
このことを,数学の言葉では「実数の集合と数直線上の数は一対一対応している」と言います.
実数の集合が四則演算(たし算,ひき算,かけ算,わり算)について閉じていることは簡単に確かめられます.
Q.
有理数の集合上でも実数の集合上でも四則演算は定義できます.
この二つの集合は,どのような点で決定的に違うのでしょうか?
A.
第二回 ≦ と < の小さな違い・大きな違い をcheck!
長旅お疲れ様です.
数の世界の冒険はひとまずここでおしまい.
計算(演算)とは何か?
数の世界の旅を通じて,知ってもらいたかったことは,
ということです.
私たちが日々「アタリマエ」に使っている計算の根拠・計算できる理由が,この旅を通じて少しは実感できましたか?
(今回はわかりやすさ重視で「演算」から「集合」を見つけましたが,本来は「集合」から「演算」が定義されます.)
今回のような「アタリマエを掘り下げる」行為は,科学的な精神にほかなりません.
常日頃「アタリマエとは何か?」について考えながら生活をすると,まったく新しい世界が見えてくることでしょう.
広大な世界へ...
かけ算の順序問題
皆さんは「かけ算の順序問題」をご存じでしょうか?
Q.
リンゴが3個ずつ入った袋が全部で4袋あります.
リンゴは全部でいくつありますか?
A1. 3×4=12(個)
A2. 4×3=12(個)
A1.とA2.はどちらも同じ答えを導き出していて,両方正解に見えます.
かけ算の順序問題は,ある小学校の教員が(ans.2)の解答にバツをつけたことから勃発しました.
具体的な内容は以下の動画やリンクを参照してください.
(特に以下の動画は皆さんに見てほしいです!!)
とある東大生はかけ算に順序が必要だと考えます|Nao Harada|note
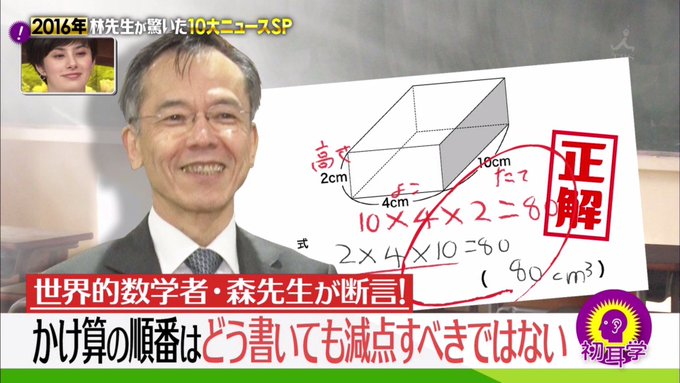
上記の通り,いろいろな意見があります.
一概にどちらが正しいとは言えませんが,私はこの問題について「考える意味がない」と考えます.
それらは定義の問題で,人によって意見が変わってくるのは明白です.
皆さんはどう考えますか?
まとめ
今回のキーポイント
- 四則演算の順序をcheck
- 演算が集合に関して閉じていることが重要
- 自分が「アタリマエ」だと思っていることを常に疑う → 科学的な精神
最後までご覧いただきありがとうございました.
次回の記事もお楽しみに!
オリジナル版はこちら↓
参考文献
wikipediaいろいろ
いらすとや-https://www.irasutoya.com/
数の起源-http://www7a.biglobe.ne.jp/~number/page1.html
ニコニコ大百科-https://dic.nicovideo.jp/a/6%C3%B72%281%2B2%29
高校数学の美しい物語-https://mathtrain.jp/
その他文中のリンク
「読んでみた」シリーズ プロローグ
これから始まる「読んでみた」シリーズの紹介記事です.
「読んでみた」シリーズとは?
「読んでみた」シリーズでは,数学が好きな高校生である私Fが,今までに読んだ本(主に数学書)の感想・解説を書きます.
しかしながら,私もまだまだブログ・数学初心者です.
自分自身の文章力や数学力のレベルアップも兼ねて,記事作成を頑張ります.
わかりにくい表現・用語などがあれば,指摘してもらえると嬉しいです.
今後ともよろしくお願いいたしますm(__)m
本の紹介
現在執筆中の記事は,
の四冊です.それぞれの本について簡単に説明します.
『数論への招待』
一つ目の『数論への招待』は,月刊雑誌『数学セミナー 』で2年半にわたって連載された記事を,一冊の本としてまとめ上げたものです.
三角形と素数の「神秘的」なつながりから,現代数学の一大テーマである「p進数」の世界へと誘う,素敵な本です.
独特な表現や語り口が癖になります.高校生でも楽しく読めます.
また,著者の加藤和也さんは数学の分野の一つである「整数論」の世界的権威でもあります.
p進数の世界は,昼間の星のように,めだたない見えにくいものです.けれども本当はこの宇宙は,そういう見えにくいもので支えられているのでしょう.
――― 加藤和也著「数論への招待 第2章 実数とp進数」より引用

『具体例で親しむ高校数学からの極限的数論入門』
二つ目の『極限的数論入門』は,関西を中心に勢力を拡大している予備校「研伸館」の現役講師である著者が,高校生にもわかりやすく,無限和や無限積,面白い性質を持つ数たちについて説明しています.
タイトルに含まれる「具体例で親しむ高校数学からの」からもわかるように,手を動かし具体例を確かめながら読むと,より楽しめる本です.高校生でも気軽に読めます.
深く考えれば,どんな数学も楽しいものです.いろいろな具体例を考えていくことで,どんどん理解が深まるものです.そして親近感がわいてくるはずです.
――― 吉田信夫著「極限的数論入門 まえがき」より引用

『数学オリンピックチャンピオンの美しい解き方』
三つ目の『数学オリンピックチャンピオンの美しい解き方』は,あらゆる物事に通じる「問題解決の方法」を学べる良書です.
数学オリンピックを目指している人はもちろん,美しい数学に触れたい人にはお勧めです.
また,著者のテレンス・タオ氏は,国際数学オリンピック金メダリストに12歳の若さで輝きました.その才能衰えることなく,2006年には数学界のノーベル賞と呼ばれる「フィールズ賞」を受賞しました.天才すぎます...
(実はこの本は,テレンス・タオ氏が15歳の時に書いたものなんです...ひえぇ...)
古代ギリシアの哲学者プロクロスはこう言った.
「これが,ゆえに,数学なのである.数学は,目に見えない魂の形を思い出させる.数学は自分自身の発見物に生命を吹き込む.数学は私たちの心を目ざめさせ,知性を浄化する.数学は私たちの本来の考えを明るみに出す.数学は生まれながらの私たちの忘却と無知の状態に終止符を打つ.」
しかし私が数学を好きなのはただそれが面白いからである.
――― テレンス・タオ著「数学オリンピックチャンピオンの美しい解き方 初版へのまえがき」より引用

『東大の数学入試問題を楽しむ』
四つ目の『東大の数学入試問題を楽しむ』は,日本が誇る「東京大学」が今までに出題してきた数学入試問題を,著者が自分自身の思想や所感を絡めて紹介・解説している本です.
過去・現在・未来の情勢を,著者がユニークな切り口語り口で論じているので,数学が苦手な人にとっても,ひとつの完成された「エッセイ(もしくは評論)」として十二分に楽しく読めます.
著者である長岡亮介氏は,趣味に『数学教育』を挙げるほどの教育熱心な人で,数学の本質(社会の本質?)を伝えようとする一貫した姿勢は,本文中にも随所に表れています.
実は,今日,「理系 vs. 文系」という分類自身が,すでに古くさい.
(中略)
今日のような複雑化した社会の中で,新領域を開拓していくためには,干涸びた類型にとらわれない自由な発想と,その発想を支える幅広い教養が必須である.他人と同じ発想をし,同じ規範で行動する,要するに,世間と時代に阿る態度では,到底,現代の困難を打開することはできるはずがない.
――― 長岡亮介著「東大の数学入試問題を楽しむ 第9話 理系 vs. 文系?!」より引用
筆者は,次世代を担う青年には,自分の人生はもちろん,社会の未来を切り拓く心構えと責任感をもってほしいと願う.
(中略)
「大の大人たち」すら「子供扱い」するこの国では,若者に対しては,もっとひどい子供扱いが罷り通っていることにも気づいてほしい.
――― 長岡亮介著「東大の数学入試問題を楽しむ 第29話 大人扱いの苦手な近年の日本」より引用

今回は「簡単な紹介」なので,専門用語などの説明は省きました.
詳しい解説などは,次回以降の「読んでみた」シリーズでおこないますので,ご期待ください.お楽しみに...
最後までご覧いただきありがとうございました.
次回の記事もお楽しみに!!
世界で一番難しい論理パズルに挑戦 part.1
はじめての数学記事です.お手柔らかに...
世界で一番難しい論理パズル
まずはこちらの動画をご覧ください.(答えを見たくない方は問題設定だけでも確認してください)
これは,2019年5月24日(金)に開催された「数学デー」というイベントで取り上げられた論理パズルです.
数学デーとは,東京では週二回,大阪では週一回開催している数学のイベントです.
なので,愛知県在住の私は残念ながら参加できません...
その代わりに,たまに更新される「数学デー」Channel - YouTubeを見て,数学デーの雰囲気を味わっています.
余談はさておき,「世界で一番難しい論理パズル」について紹介します.
二人の幼女AとBがいます.
悪魔が幼女Aにひとつの数を告げ,適当にポーンのおかれたチェス盤を見せます.
幼女Aはチェス盤(4×4)にポーンをひとつ置くか,ひとつ取り除くかして,悪魔に告げられた数を幼女Bに伝えなくてはいけません.
さて,どうすればよいでしょうか?
――― 「世界で一番難しい論理パズルを実践してみた」 概要欄より
内容を(動画の内容に合わせて)分かりやすくまとめると,
- 登場人物は,M(悪魔) A(幼女) B(幼女)の3人.
- Mは4×4の上下左右が区別できる盤面上に適当な点を打ち,さらに1つの数(0~15)をAに告げる.
- Aは盤面上の点を1つ増やすか減らすかする.
- Bが盤面だけを見て数を当てる方法を述べよ.
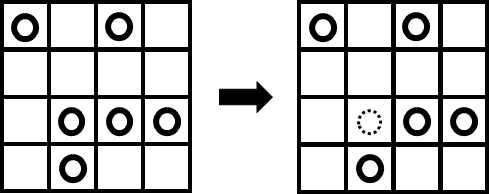
この問題はパッと見,漠然とした条件しか与えられておらず,解けそうにありません.
しかし実は,ちゃんとした解答が存在します.
時間に余裕のある方はぜひ,腕試しがてらに考えてみてください.
初回なので,今回の記事は短いですがここまで.
part.2 では,この論理パズルの解説をします.
最後までご覧いただきありがとうございました.
次回の記事もお楽しみに!
――――――――――――――――――――――
問題のヒントです
ヒント1 2進数を使う
ヒント2 mod(合同式)の考え方を使う
はじめまして
はじめての記事
若さというのはまじで武器
— 牟田口廉也 (@ezo_ninja) 2020年2月4日
大学院生が自我がどうとか、シナプス結合がどうとか言っても何も驚かれないけど、高1が言うと天才扱いされたりする
実際は前倒してるだけだから何も凄くないんだけどねw
所詮研究じゃなくて勉強だから
グレタも同じで、あれを婆さんが言っても狂人のたわごとと思われるだけ
上記のTweetがとても印象に残っています.
私はそれほど若くはないしそれほど才能もないけれども,インターネットの世界で見かける,いわゆる「ギフテッド」のような人たちに刺激を受け,(主に数学に関して)学んだことや,発見したことをどこかに残したいと思うようになりました.
(本当は,新型コロナウイルスの影響で高校が休校になってしまい,暇つぶしに記事を書いています.皆さんもこんな機会なんてめったにないですから,ブログをはじめてみては?)
ここでやりたいこと
現在高校2年生(新高校3年生)の私は,
・受験数学
・競技数学
・大学教養数学
・プログラミング
・その他数学の多分野
などについて学んでいる途中です.これらのことに関して,ひとまずは
となるよう意識します.
読者の健全な理解のためには,自分自身の理解が必要になるからです.(もちろんわかりやすい記事になるよう,できる限り努力はします!)
このように,しばらくは「備忘録」のような使い方をします.
「それならブログじゃなくてもいいんじゃない?」と考える人もいるかもしれません.
しかし,パブリックな空間に自分の知識・思考をさらすことによって,それらにもっと磨きをかけられると思うので,あえてブログをはじめます.
わかりにくい点や改善点などあればどしどしコメント欄へご記入ください.
そんなこんなで
そんなこんなで,強い意志もなく,なんとなくはじめてみました.
今後とも「Fの数学メモノート」を宜しくお願い致しますm(_ _)m
はじめての数学記事はこちら⤵

